When fluid flows past an obstruction, it creates swirling patterns that reveal precise flow rates. This natural phenomenon powers over 2 million industrial vortex meters worldwide.
The working principle of vortex flow meters is based on the von Kármán effect where alternating vortices shed from a bluff body at a frequency proportional to flow velocity. The meter counts these vortices (typically 1-3000 Hz) and converts them to flow rate using the formula: f = St × v/d where St is Strouhal number (~0.2), v is velocity, and d is bluff body width.
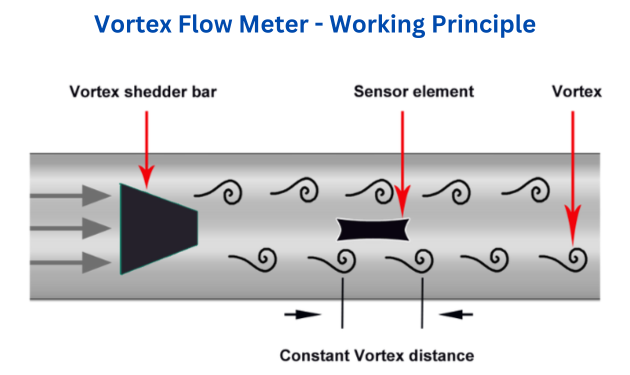
Vortex Formation Process
This deceptively simple principle hides complex fluid dynamics. Let’s examine the physics behind this precise measurement technology.
What Is the Principle of Operation of a Vortex Flow Meter?
Four-stage vortex generation:
Vortex Shedding Process
-
Boundary Layer Separation
- Fluid splits at bluff body leading edge
- Velocity differential creates shear layers
- Pressure imbalance initiates roll-up
-
Vortex Formation
- Rotational flow develops downstream
- Alternating left/right rotation
- Fully formed within 3-5 pipe diameters
-
Detachment & Convection
- Vortices break free at fixed frequency
- Travel downstream with flow
- Maintain structure for 10D+
-
Detection & Counting
- Piezoelectric sensor measures pressure pulses
- Capacitive sensors detect density changes
- Ultrasonic monitors acoustic signatures

Vortex Lifecycle
Key Design Elements
| Component | Function | Material Options | Critical Parameters |
|---|---|---|---|
| Bluff body | Generates vortices | 316SS, Hastelloy | Width (20-30% ID) |
| Sensor | Detects vortices | PZT, PVDF | Sensitivity (<1Pa) |
| Shedder bar | Enhances shedding | Tungsten carbide | Edge sharpness (Ra<0.8µm) |
| Body | Houses components | Carbon steel, 304SS | Pipe size match (±1%) |
Flow Profile Requirements
- Minimum 15D straight upstream
- 5D downstream for stabilization
- Reynolds number >10,000 for St stability
- Velocity 0.3-9 m/s (liquid), 4-80 m/s (gas)
What Is the Working Principle of a Flow Meter?
Measurement Technology Comparison:
Primary Flow Measurement Principles
| Type | Working Principle | Accuracy | Best For |
|---|---|---|---|
| Vortex | von Kármán effect | ±1% | Clean liquids/gas |
| Turbine | Rotor revolutions | ±0.5% | Low-viscosity |
| Magnetic | Faraday’s Law | ±0.5% | Conductive |
| Ultrasonic | Transit time diff | ±0.25% | Large pipes |
| Coriolis | Mass flow effect | ±0.1% | High-value |
Vortex Specific Advantages:
-
No Moving Parts
- Bluff body fixed
- Sensor non-intrusive
- Minimal wear
-
Wide Compatibility
- Liquids: Water to cryogenics
- Gases: Air to natural gas
- Steam: Saturated/superheated
-
Direct Measurement
- Measures actual velocity
- Insensitive to density changes
- Linear frequency output

Measurement Methods
Limitations to Consider:
- Minimum Flow: Requires Re>10,000
- Vibration Sensitivity: Mechanical interference
- Pipe Size: Best below 300mm
- Viscosity: Limited to <30cSt
- Multi-phase: Not recommended
What Is the Principle of the Vortex?
Fluid Dynamics Fundamentals:
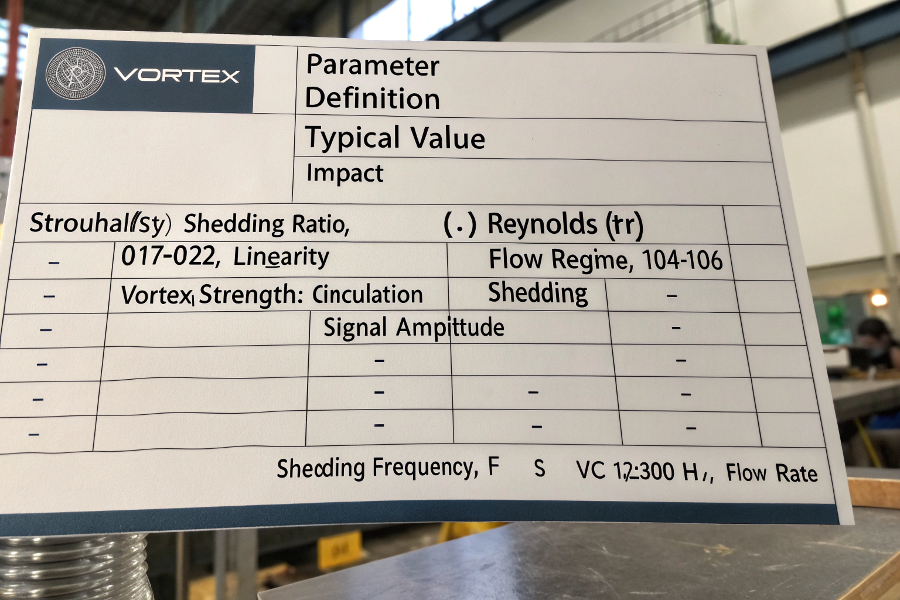
Vortex Physics Parameters
| Parameter | Definition | Typical Value | Impact |
|---|---|---|---|
| Strouhal (St) | Shedding ratio | 0.17-0.22 | Linearity |
| Reynolds (Re) | Flow regime | 10⁴-10⁶ | Shedding start |
| Vortex strength | Circulation (Γ) | 0.1-5 m²/s | Signal amplitude |
| Shedding freq | f = St×v/d | 1-3000 Hz | Flow rate |
Three Vortex Formation Theories:
-
Instability Theory
- Shear layer oscillations
- Feedback loops
- Natural resonance
-
Pressure Differential
- Low pressure behind bluff body
- Alternate side switching
- Bernoulli effects
-
Conservation Laws
- Angular momentum
- Kelvin’s theorem
- Vorticity transport
Fluid Dynamics
Mathematical Relationships:
-
Strouhal-Reynolds Correlation
St = a + b/Re^c
(a≈0.2, b≈-5, c≈0.5) -
Vortex Frequency Calculation
f = (St × v)/D
Where:
v = flow velocity (m/s)
D = bluff body width (m) -
Energy Equations
E = ½ρv² × shedding volume
P = E × f
What Is the Vortex Flow Theory?
Industrial Measurement Applications:
Vortex Meter Performance Data
| Fluid Type | Velocity Range | Accuracy | Special Considerations |
|---|---|---|---|
| Water | 0.5-7 m/s | ±1% | Bubble sensitivity |
| Natural gas | 5-50 m/s | ±1.5% | Pressure compensation |
| Steam | 15-75 m/s | ±2% | Temperature effects |
| Chemicals | 0.3-5 m/s | ±1.25% | Material compatibility |
Advanced Measurement Techniques:
-
Dual-Sensor Designs
- Noise cancellation
- Phase comparison
- Redundancy
-
Smart Signal Processing
- FFT analysis
- Adaptive filtering
- AI pattern recognition
-
Hybrid Systems
- Vortex + DP
- Vortex + temp
Feature Basic Meter Advanced Meter Smart Meter Strouhal adjustment Fixed Manual Auto-tune Signal processing Analog Digital AI-based Output options 4-20mA HART+FF Wireless+IoT

Field Installations
Future Developments:
- Micro-vortex for low flow
- Nanomaterial bluff bodies
- Quantum sensors for detection
- Predictive maintenance integration
Conclusion
Vortex flow meters transform the natural von Kármán effect into precise measurement through controlled vortex shedding (1-3000Hz), delivering ±1% accuracy for liquids, gases, and steam. Their bluff body design and advanced signal processing convert fluid dynamics into reliable flow data without moving parts, making them ideal for industrial applications where maintenance simplicity matters as much as measurement accuracy.
