Getting flow measurements wrong can lead to serious process control issues and inefficient operations.
Differential pressure and flow rate have a square root relationship, where flow rate is proportional to the square root of the differential pressure according to Bernoulli’s principle.
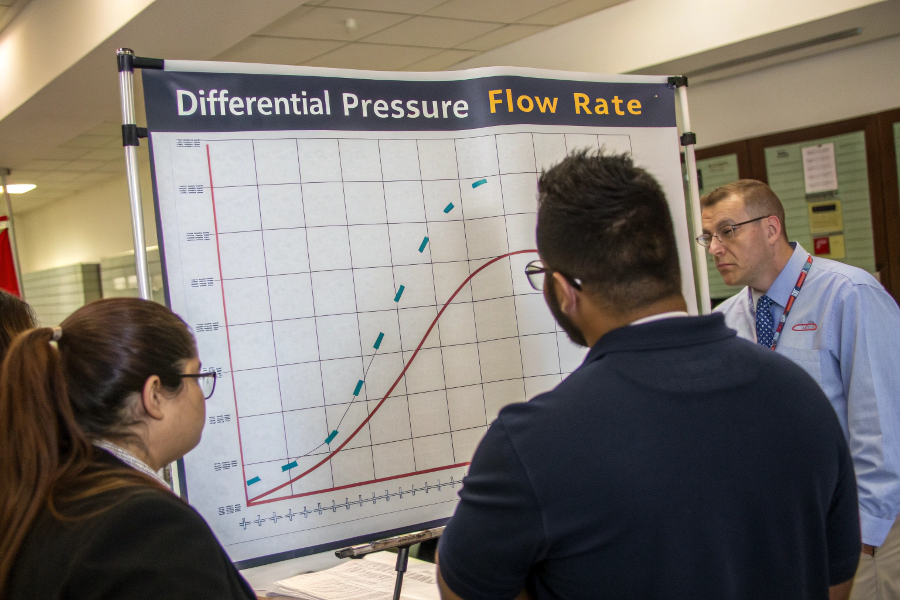
DP and Flow Rate Relationship
Let me explain this fundamental relationship based on our extensive experience with flow measurement.
How Is Differential Pressure Related To Flow Rate?
Many engineers struggle to understand the precise relationship between DP and flow.
When fluid flows through a restriction, the pressure difference created is proportional to the square of the flow rate, following the equation Q = K√ΔP, where Q is flow rate and ΔP is differential pressure.

DP Flow Equation Diagram
From my years of working with flow measurements:
Basic Principles
Key Factors
Parameter Symbol Relationship Flow Rate Q Dependent variable Differential Pressure ΔP Independent variable Flow Coefficient K Constant Density ρ Affecting factor Influencing Elements
- Pipe diameter
- Fluid properties
- Temperature effects
- Pressure conditions
Practical Applications
Common Uses
- Pipeline monitoring
- Process control
- Custody transfer
- Equipment protection
Implementation Considerations
- Accuracy requirements
- Installation conditions
- Maintenance needs
- Calibration frequency
What Is The Relationship Between DP And Flow?
Understanding the mathematical relationship helps in accurate flow measurement.
The relationship follows Q = K√ΔP, meaning doubling the flow rate requires four times the differential pressure, demonstrating a non-linear relationship.
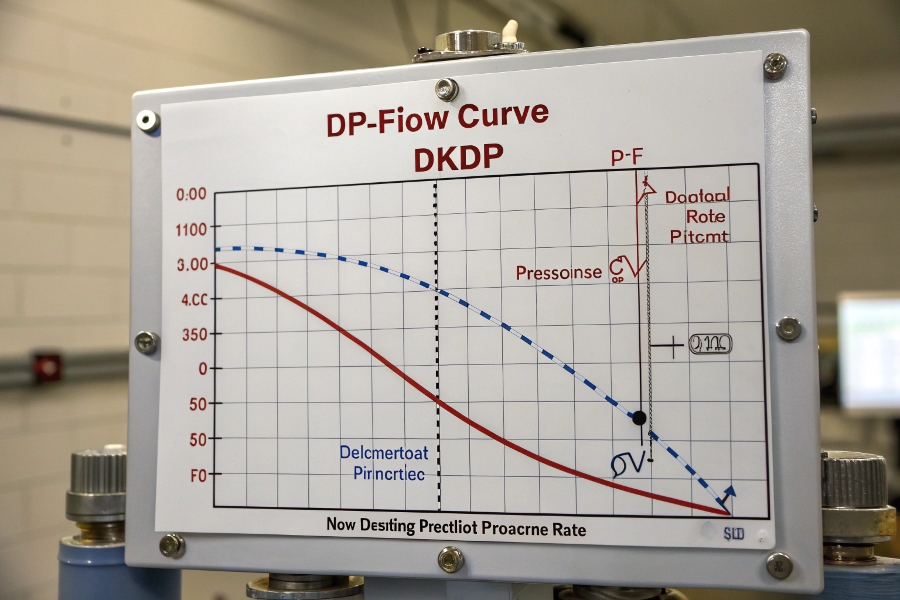
DP vs Flow Rate Curve
Based on our field experience:
Mathematical Analysis
Relationship Components
Factor Effect Impact Square Root Non-linear Measurement range K Factor Calibration Accuracy Reynolds Number1 Flow profile Calculation Beta Ratio Sizing Range ability Critical Parameters
- Fluid velocity
- Pipe roughness
- Viscosity effects
- Temperature influence
Application Impact
Design Considerations
- Range selection
- Turndown ratio
- Accuracy needs
- Response time
Operational Factors
- Pressure loss
- Energy consumption
- Maintenance requirements
- Cost implications
What Is The Relationship Between Pressure And Flow Rate?
Process engineers often need clarity on pressure-flow dynamics.
Pressure and flow rate are related through Bernoulli’s equation, where total pressure remains constant but converts between static and dynamic pressure as flow velocity changes.

Pressure and Flow Relationship
Drawing from our technical expertise:
Physical Principles
Pressure Components
Type Description Relationship Static At rest Decreases with flow Dynamic2 In motion Increases with flow Total Combined Remains constant Loss3 Friction Increases with flow
- Flow Characteristics
- Laminar vs turbulent
- Pressure drop
- Energy conservation
- Flow resistance
Practical Implementation
Measurement Considerations
- Tap location
- Installation effects
- Calibration needs
- Accuracy requirements
System Design
- Pipe sizing
- Material selection
- Installation points
- Maintenance access
How Do You Convert DP To Flow?
Converting DP readings to flow rates requires understanding specific calculations.
To convert DP to flow rate, use Q = K√ΔP and apply correction factors for fluid density, temperature, and pressure conditions.

DP to Flow Conversion
Based on our calculation experience:
Conversion Process
Calculation Steps
Step Action Purpose Measure DP Get reading Input value Apply K factor Calculate Base flow Density correction Compensate Real conditions Temperature correction Adjust Actual flow Required Information
- Calibration data
- Process conditions
- Fluid properties
- Installation details
Practical Application
Conversion Tools
- Calculator methods
- Software programs
- Field devices
- Manual calculations
Quality Checks
- Verification steps
- Error analysis
- Documentation
- Periodic review
Conclusion
Understanding the square root relationship between differential pressure and flow rate is crucial for accurate flow measurement, proper instrument selection, and effective process control.
Exploring the Reynolds Number helps in understanding fluid dynamics, which is essential for accurate flow profile calculations in engineering. ↩
Understanding dynamic fluid behavior is crucial for applications in engineering and physics, enhancing your knowledge of fluid dynamics. ↩
Exploring pressure loss in fluid systems can help you optimize designs and improve efficiency in various engineering applications. ↩



